図形のルールと移動について

２点A,Bを両端とするまっすぐな線のことを、線分ABと呼びます。

２点A,Bを通るまっすぐな線のことを、直線ABと呼びます。

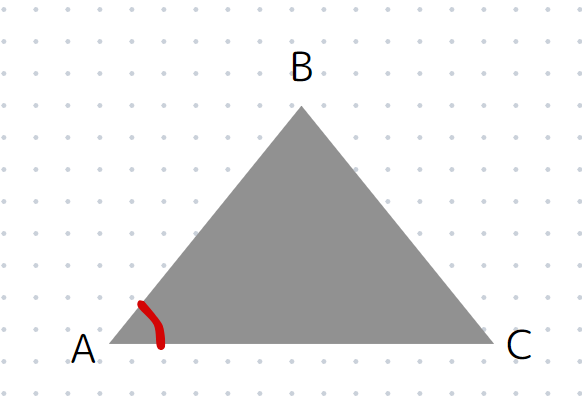
角を表すときは∠という記号を使います。

図のような角Aを表したいときは∠Aと表すことができます。

しかし、ほとんどの場合は、∠BACのように、B→A→Cの時にできる角というように書くことが一般的です。

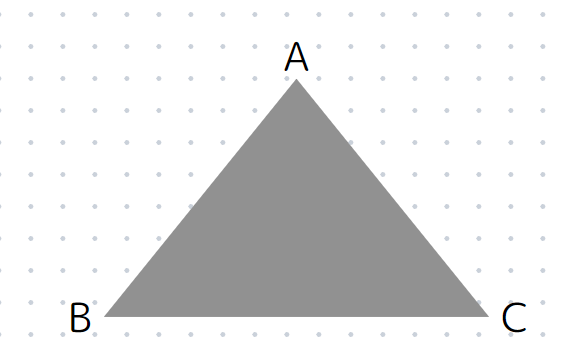
3点A,B,Cを頂点とする三角形を書くときは、頂点がA→B→Cの順番で結べば出来るので、△ABCと表すことができます。

このとき、逆回りに△ACBとしてもOKです。

四角形になっても同じです。頂点がA→B→C→Dの順番で結べば出来るので、四角形ABCDと表します。もちろん四角形ADCBでもOKです。

このように、多角形は頂点を結ぶとその図形が書けるように表現していけばOKです。

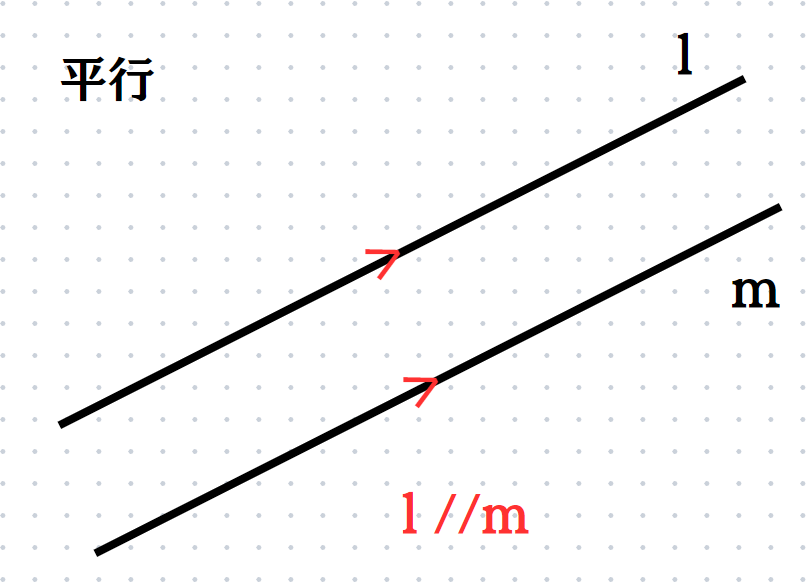
2つの直線が交わらない状態の時、2つの直線が平行であると言います。

この時はｌ//ｍというように表します。

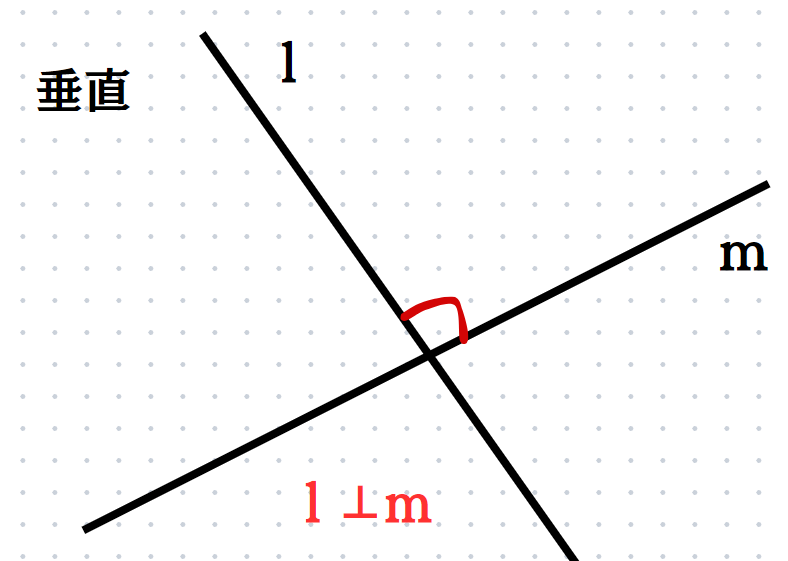
2つの直線が直角に交わっているとき、2つの直線が垂直であるといいます。

この時はｌ⊥ｍというように表します。

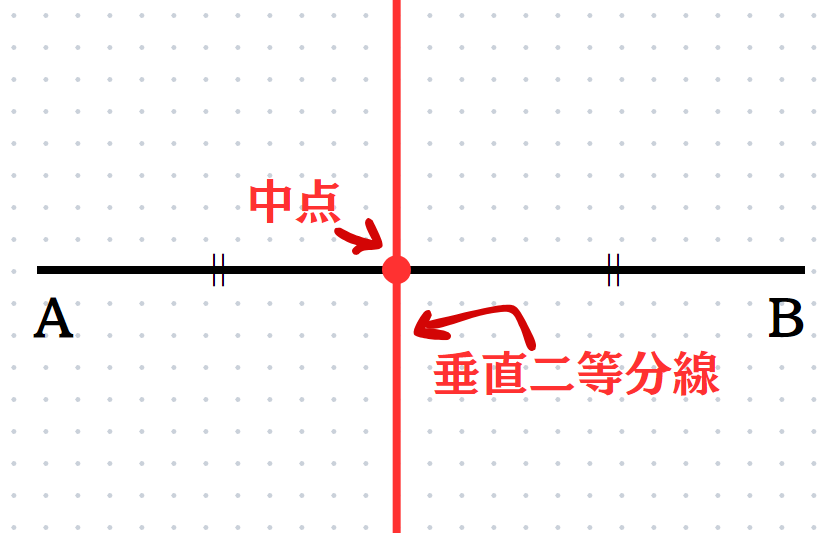
線分ABの真ん中の点を線分ABの中点といいます。

また、線分ABの中点を通り、線分ABに垂直な直線を、線分ABの垂直二等分線という。

次の図の△ABCを、点Aが点A’の位置にくるように平行移動してできる△A’B’C’をかけ、

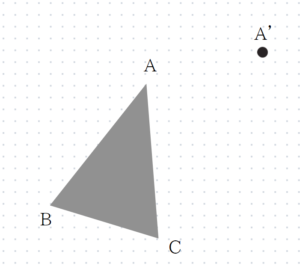
まずは平行移動ですね。書き方の手順を紹介します。

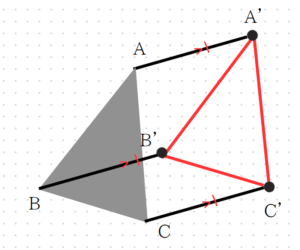
1. まず、点Aと点A’を結びます。
2. 次に、点Bを通りAA’に平行な直線と、点Cを通りAA’に平行な直線を引きます。
3. AA’の長さをものさしで測って、BB’、CC’がAA’と同じ長さになるように点B’と点C’をとり、3点A’、B’、C’を結びます。

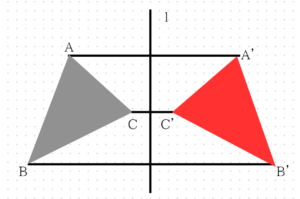
次の図の△ABCを、直線lを対称の軸として対称移動してできる△A’B’C’をかけ。

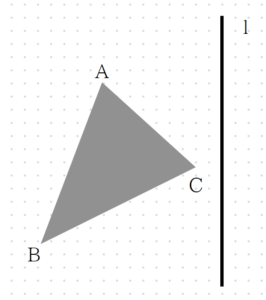
次は対称移動ですね。書き方の手順を紹介します。

1. 三角定規の片方をlにそって置き、もう片方の直角の部分をあてて点Aの通る直線を引きます。
2. 三角定規をスライドさせると、点C、Ｂを通る直線を引けます。
3. その半直線がを伸ばして、lに対しての距離が等しくなる点A’、B’、C’として結びます。

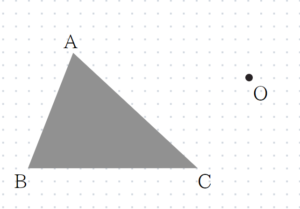
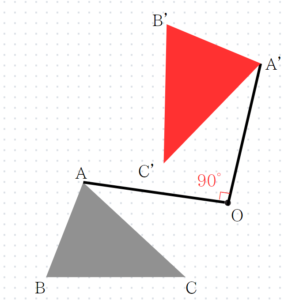
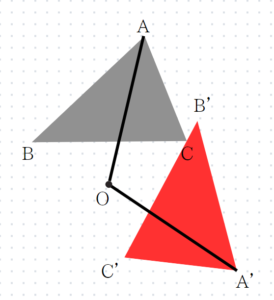
次の図の△ABCを、点Oを回転の中心として時計回りに90°回転移動させてできる△A’B’C’をかけ。

最後には回転移動ですね。書き方の手順を紹介します。

1. まず、点Oを中心に半径OAの円をかきます。
2. 次に、分度器で∠AOA’=90°となる点A’をとります。
3. 同様のことを点Bと点Cに対しても行い、点B’と点C’をとり、3点A’、B’、C’を結びます。

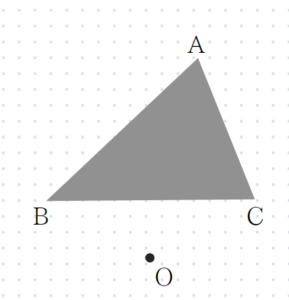
次の図の△ABCを、点Oを回転の中心として時計回りに120°回転移動させてできる△A’B’C’をかけ。