前回は「図形のルールと移動について」を学んでいきましたね。
今回からは作図を学んでいくので、定規とコンパスを用意して、実際に手を動かしながら学んでいきましょう!
5-2 正三角形・正六角形の作図
例題4 正三角形を作図せよ
作図の定義から確認していきましょう。作図とは以下のようなルールがあります。
- 目盛りの付いていない定規とコンパスだけで点や図形を書くこと。
- 長さを測ってはいけない。
- 分度器を使ってはいけない。
- 無地の紙に書く。
ということです。正三角形とは3つの辺と角度がそれぞれ等しい三角形のことでしたね。
以下の3つのSTEPで書くことができます。
STEP1
両端をA,Bとする適当な長さの線分を書きます。

STEP2
ABの長さと同じ半径で、2点A,Bを中心にコンパスで少しだけ円を書き、その交点をCとします。
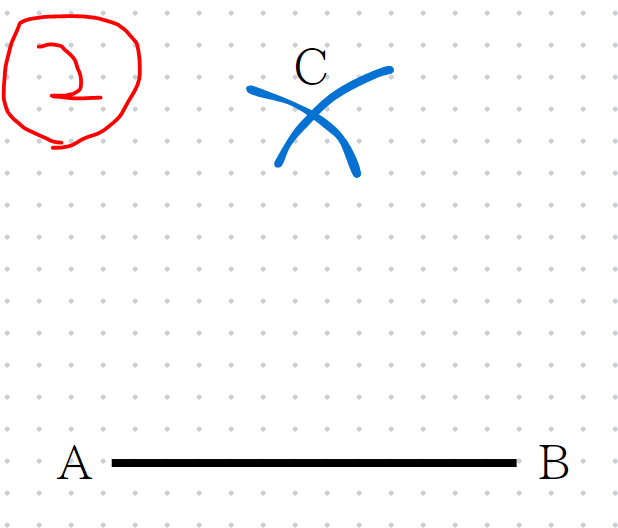
STEP3
3点A,B,Cを結ぶと『正三角形』になります。
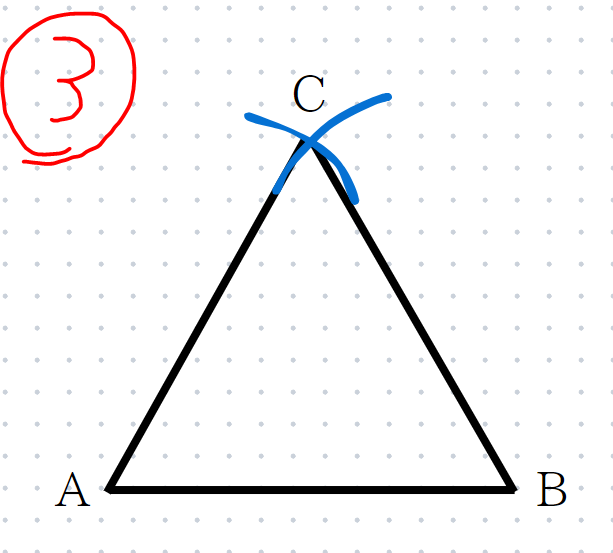
作図に使った線は必ず残しておくようにしておきましょう!
例題5 正六角形を作図せよ
難しそうですが、正六角形は5つのSTEPで書くことができます。
STEP1
適当な大きさの円を書き、円周上にAという点をとります。
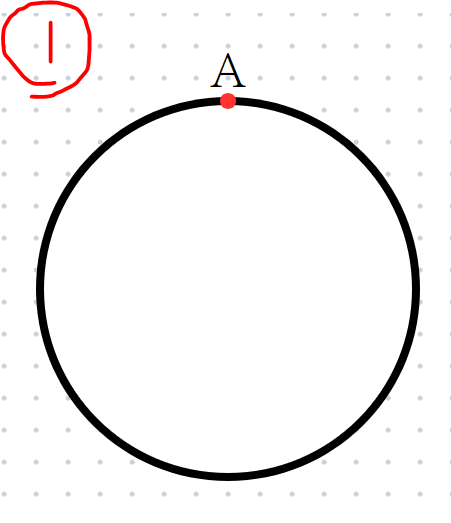
STEP2
STEP1と同じ半径で点Aを中心にコンパスで少しだけ円を書いて、交わる点をBとします。
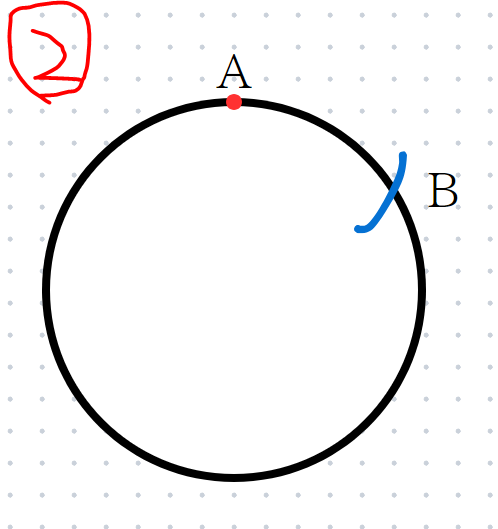
STEP3
さらに同じ半径で点Bを中心に点Aとは反対側に円を少し書いて、交わる点をCとします。
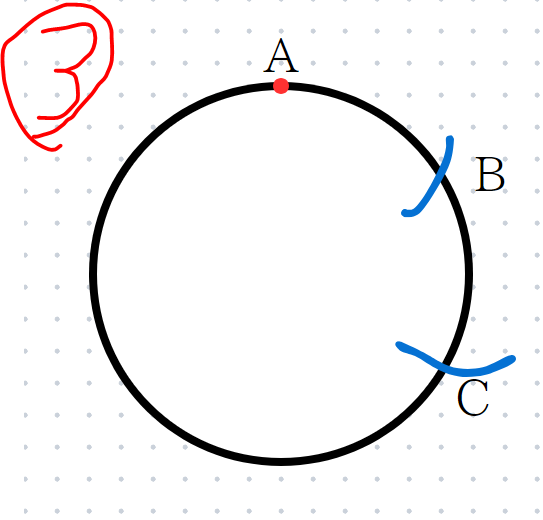
STEP4
同様にしてD,E,Fの点をとります。
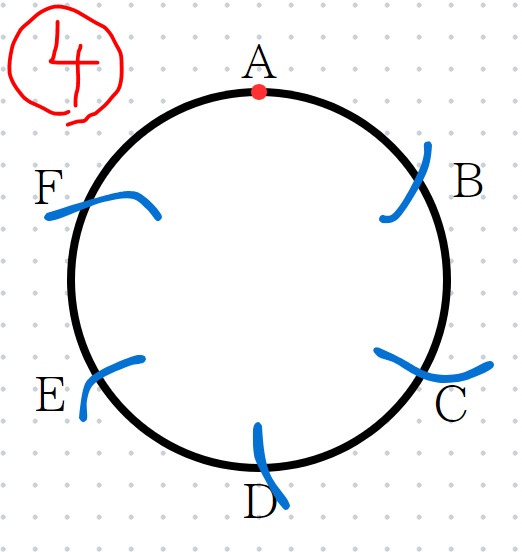
STEP5
6点A,B,C,D,E,Fを結ぶと『正六角形』になります。
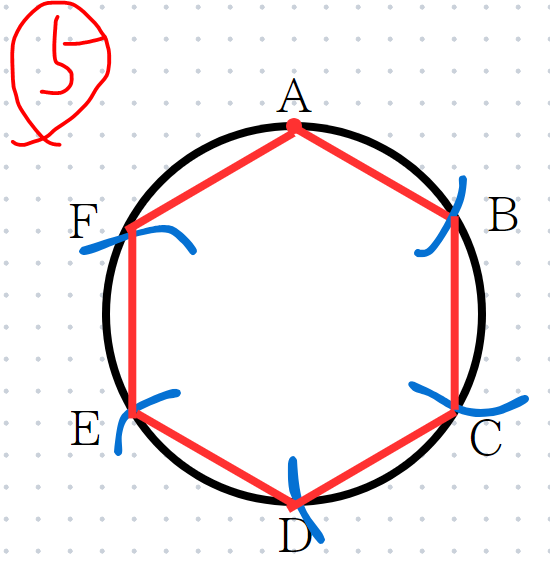
それではなぜ正六角形を書くことができたのかを考えていきましょう。
STEP1,2で行ったことは、例題4で行った正三角形を作ったことになります。
それをSTEP3,4で繰り返し行い、計6つの正三角形が集まったものが、正六角形になるんですね。
それでは、確認問題です。
確認問題68
正三角形の作図を参考にし、同じ円周上に3つの頂点がある正三角形を作図せよ。
5-3 垂線の作図
例題6
次の図で、点Aを通り、直線ℓに垂直な直線を作図せよ。
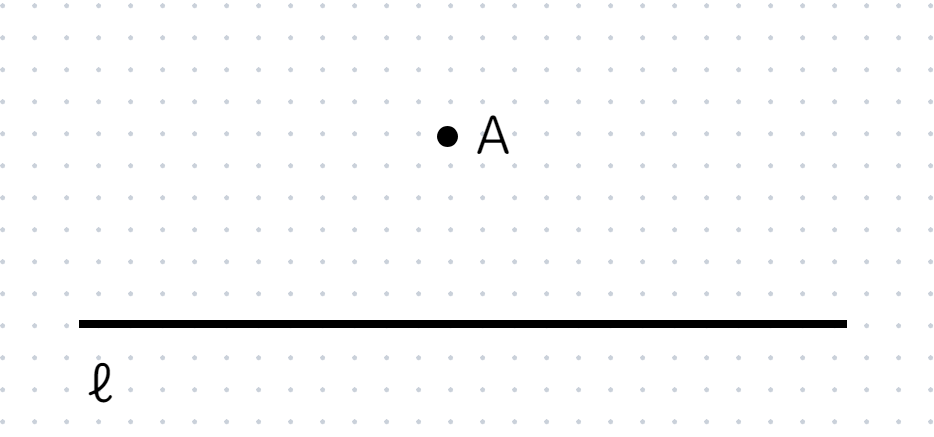
垂線とはその名の通り『垂直(90°)で交わる線』のことでしたね。
垂線の作図の仕方はいろんな方法がありますが、今回は以下の3STEPで簡単にやっていきましょう!
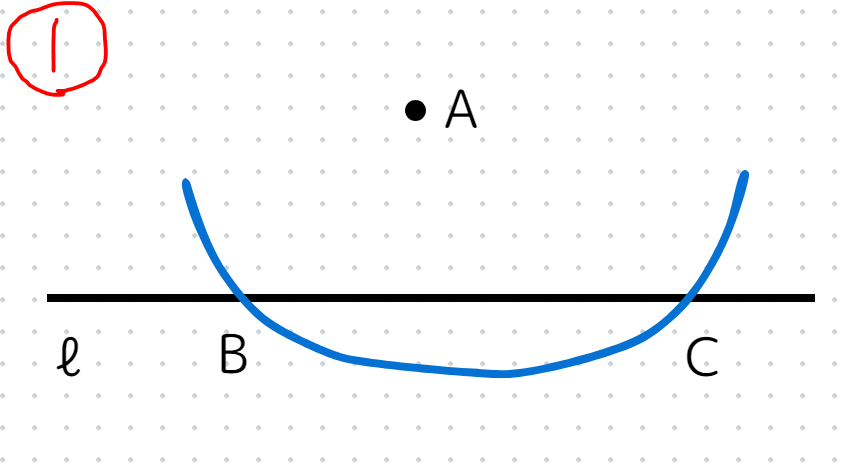
STEP1
コンパスを広げ、点Aを中心に直線と2回交わるように円を少し書いて、交点をB,Cとします。
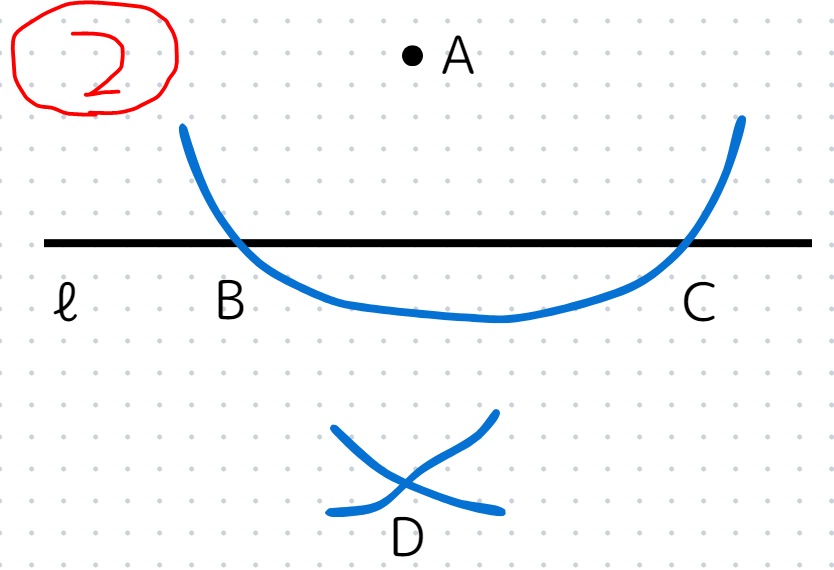
STEP2
点B,Cを中心に同じ半径の2つの円を少し書いて、交わった点をDとします。
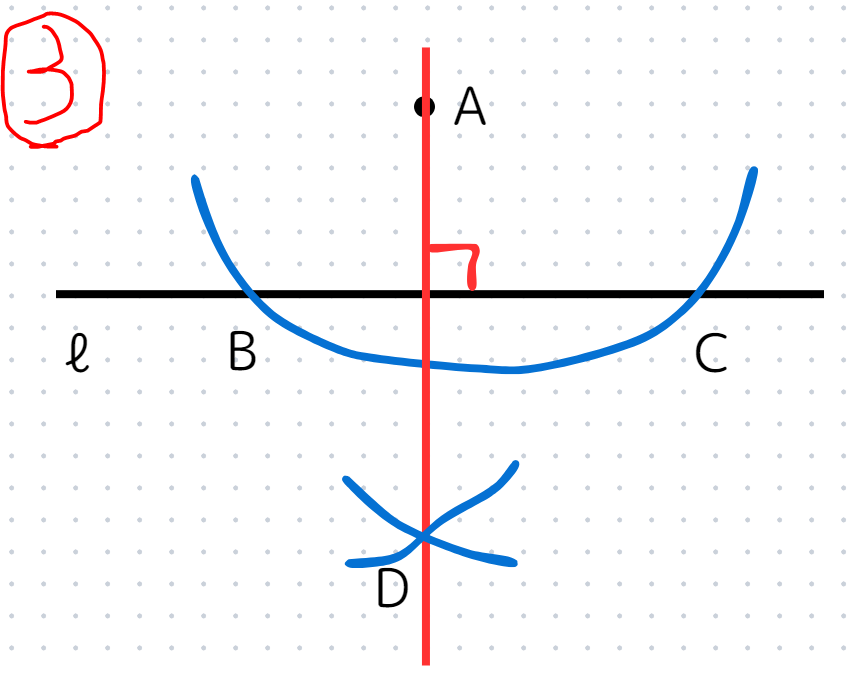
STEP3
点Aと点Dを結んだ線が、垂線になります。
さあ、今回の確認問題は少し難しいです。
初回で解けなくとも何回も挑戦してみましょう!
確認問題69
次の線分ABを1辺とする正方形を作図せよ。

いかがでしたでしょうか?
次回は「中点と垂直二等分線の作図」を学んでいきます!
それでは、また次回でお会いしましょう( ^_^)/~~~
確認問題の答え
確認問題68
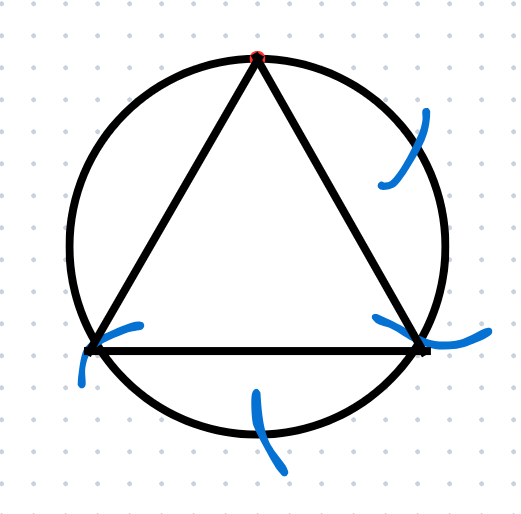
確認問題69
STEP1
点Bを通りABに垂直な直線を引く。
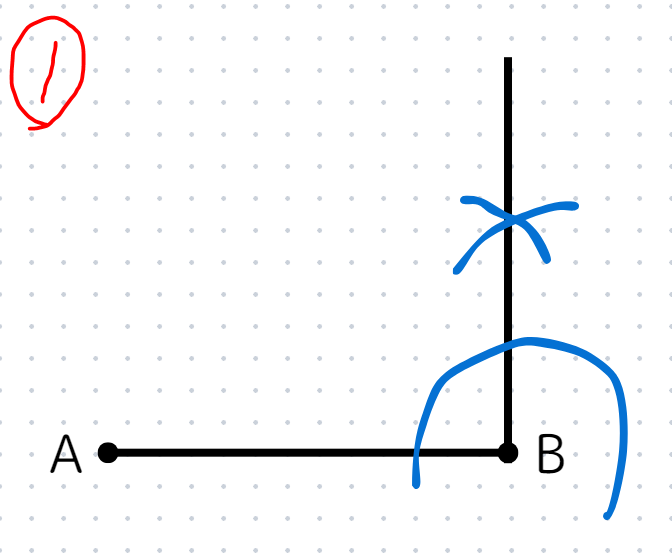
STEP2
ABと同じ長さだけコンパスを広げ、点Bを中心とした円を少し書き、STEP1で書いた直線との交点をCとする。
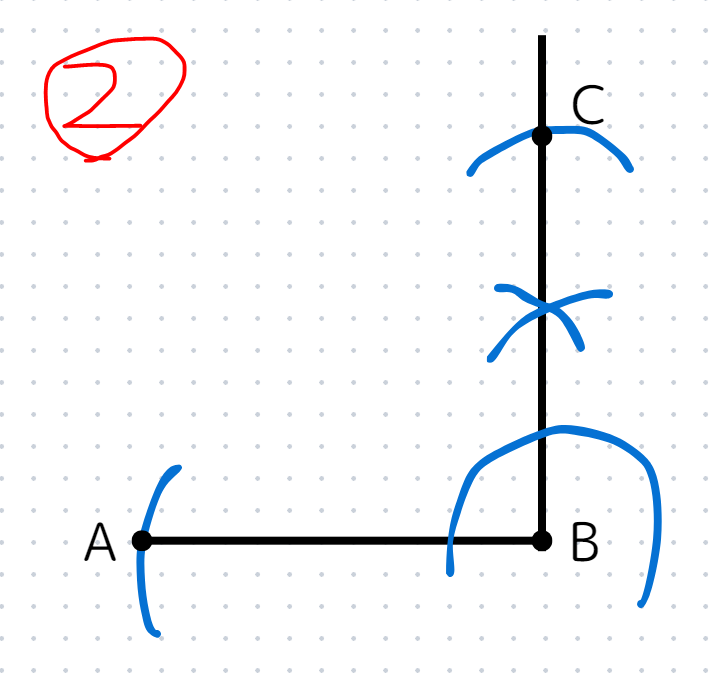
STEP3
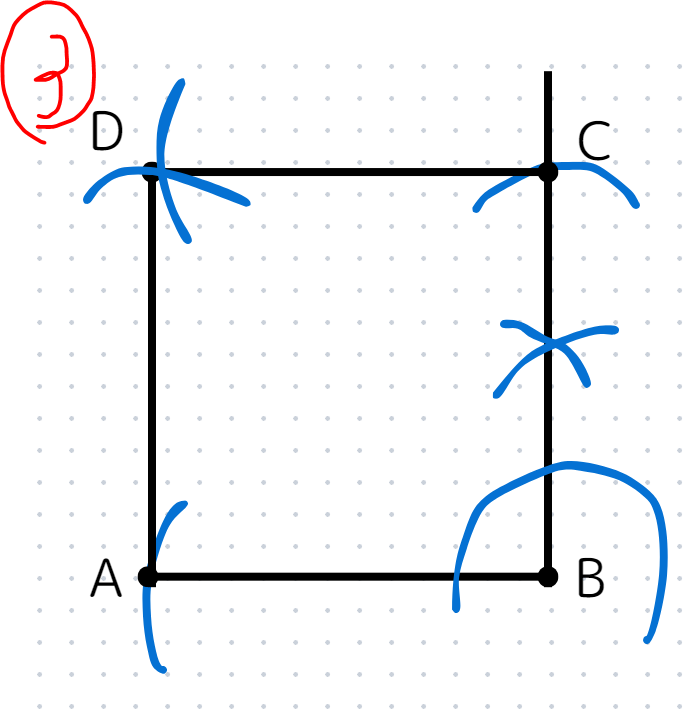
コンパスをSTEP2と同じ長さに広げたまま、点A、Cを中心とした円を少し書き、その交点をDとして4点を結ぶ。


コメント