今回は接点や、接線。角の二等分線の作図を学んでいきたいと思います。
5-5 接線と接点
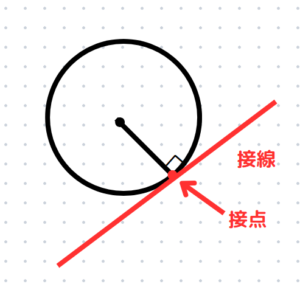
円と直線が1点だけで交わるとき、円と直線は接すると言います。この直線を円の接線と言い、接する点を接点と言います。
重要な性質として、円の中心と接点をつなぐと接線に垂直になるという性質があります。
例題9
次の図において、点Oは円の中心、直線AHは円の接線でHは接点である。∠xの大きさを求めよ。
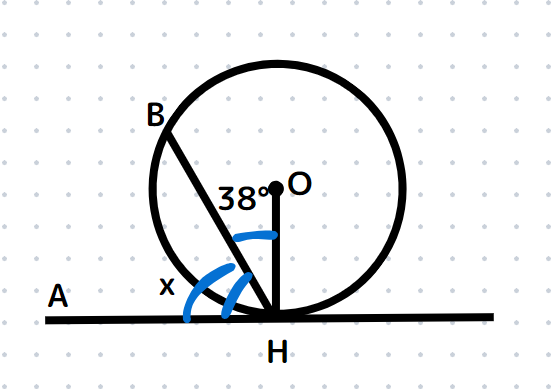
円の中心と接点をつなぐと接線に垂直になるという性質を早速使った問題です。
∠OHA=90°で、∠OHB=38°なので、
$∠x=90°-38°=52°$が答えとなります。
確認問題70
次の図において、点Oは円の中心、ℓ、mの接線である。ℓとmの交点をA、点Oからℓ、mに下した垂線をOB,OCとするとき、∠xの大きさを求めよ。
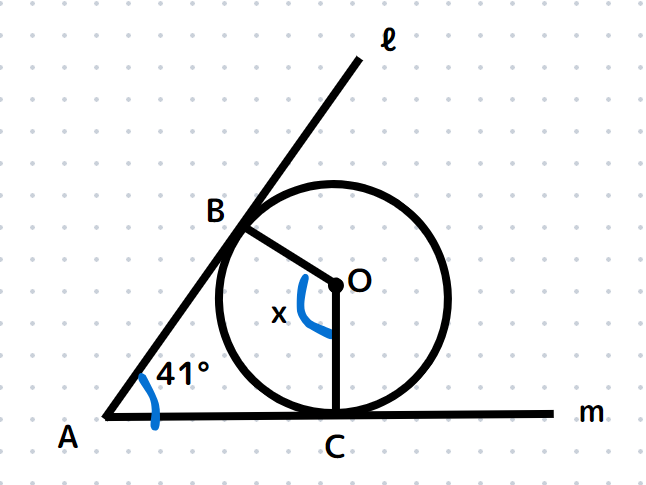
5-6 角の二等分線の作図
例題10
次の∠BACの二等分線を作図せよ。
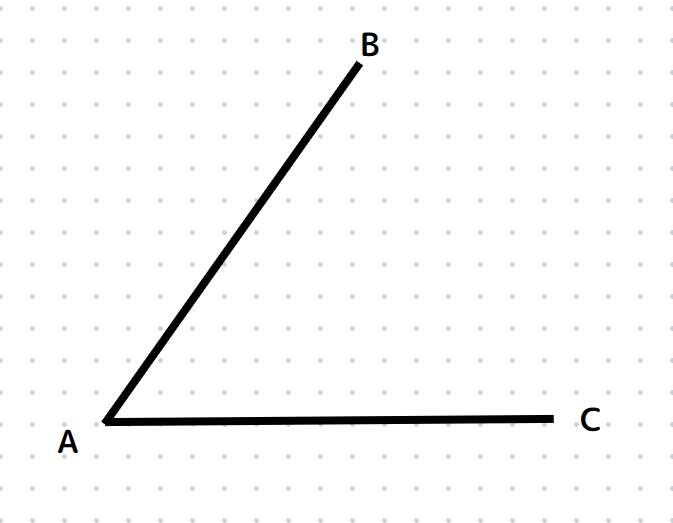
角の二等分線は以下の3STEPで作図することができます!
STEP1
適当な長さにコンパスを広げ、頂点Aを中心に2つの辺と交わるように円を書きます。
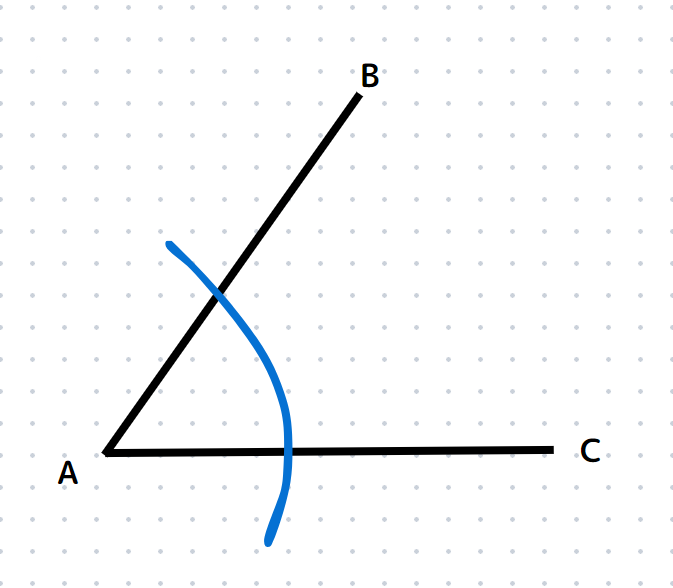
STEP2
次に、その2つの交点を中心に角の内側に少しだけ円を書き、交わるようにします。
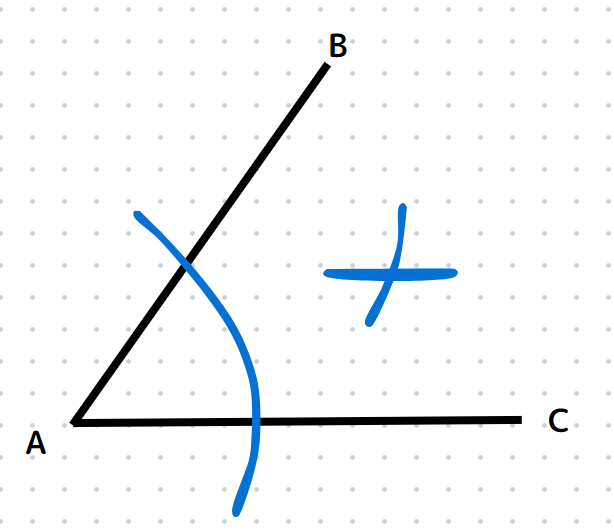
STEP3
そのときにできた交点と頂点をつなぐと、角の二等分線になります。
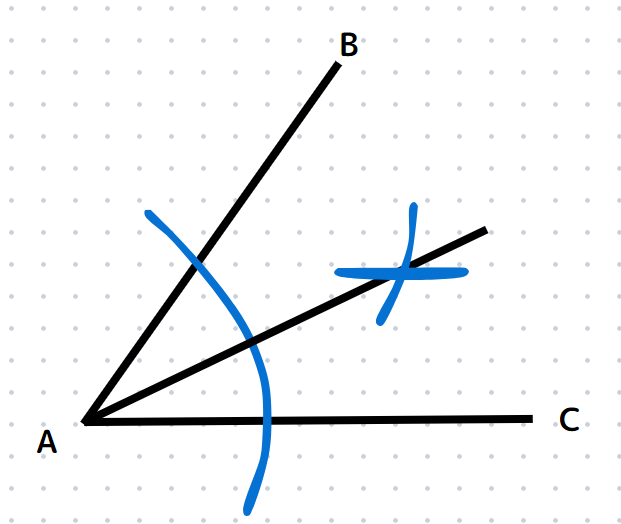
角の二等分線の重要な性質は2つあります。
- 角の二等分線上のどの点をとっても、2辺からの距離が等しくなること。
- 角の二等分線上の点を中心にコンパスを回転させると、2辺に接する円を書くことができること。
確認問題71
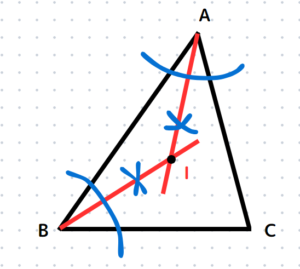
△ABCの3辺AB,BC,ACから等しい距離にある点Iを作図せよ。
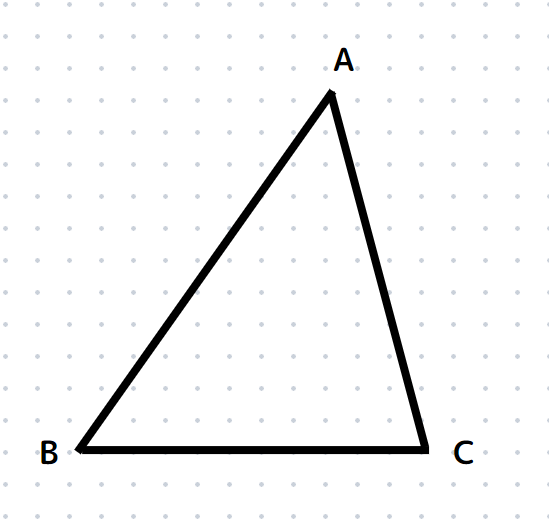
いかがでしたか?
次回はこれまでに学んだ作図をまとめをしていきます。
それでは、また次回でお会いしましょう( ^_^)/~~~
確認問題の答え
確認問題70
∠ABO=∠ACO=90°、四角形の内角の和は360°なので、
$∠x=360°-(90°+90°+41°)=139°$
確認問題71


コメント