今回より第4章、比例と反比例について勉強していきます。この単元は一次関数や二次関数といった単元につながってくるので、大切な単元になってきます。
また、小学校の頃にやった単元でもあるので、思い出しながらやっていきましょう!今回は「比例とは何か」や「座標とは何か」について勉強していきます。
4-1 比例とは
比例とは、一方が2倍、3倍となれば、もう片方も2倍、3倍となる関係のことです。
具体的にお菓子を5個ずつ配るときの、人数とお菓子の数を考えていきましょう。
人数が1人の時は、お菓子が5個
人数が2人の時は、お菓子が10個
人数が3人の時は、お菓子が15個
確かに人数が2倍、3倍となれば、お菓子の数も2倍、3倍となっていることが分かりますね。
これを文字で表すと、人数をx人、お菓子をy個とすると、
$y=5x$という式が立てられます。この形を覚えておきましょう。
一般的に比例の式は
$y=ax$と表すことができます。この時のaのことを比例定数と呼ぶので覚えておきましょう!
確認問題56 次のうち、x,yが比例の関係になっているものをすべて挙げ、その比例定数を答えよ。
(1)$y=x-7$
(2)$2x-y=0$
(3)$y=x^2$
(4)$y=\frac{x}{6}$
4-2 座標とは
小学校のころには学ばなかった概念として座標というものがあります。
場所を示す点と覚えておけば大丈夫です。この点の集まりが線になります。
そしてもう一つ覚えておくべきことは軸です。
横の線をx軸、縦の線をy軸と呼びます。これらを両方合わせて座標軸と呼びます。
そして、この二つが交わった場所を原点といいます。これも覚えておきましょう。

例題1 2点A,Bの座標を求めよ。

それでは例題を解いていきましょう。
原点から横にいくつ(x軸)、縦にいくつ(y軸)進んだかを考えればOKです。
点Aはx方向に右に2つ、y方向に上に3つ進んでいますね。
これを座標で表すと$A(2,3)$となります。
点Bはx方向に右に5つ、y方向に下に1つ進んでいますね。
ここで、x方向なら左に、y方向なら下に進むときは「マイナス方向に進む」と考えます。
よって、$B(5,-1)$が答えとなります。簡単ですね。
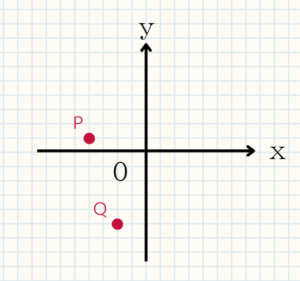
例題2 次の座標の点を図にかけ。
(1)$P(-4,1)$
(2)$Q(-2,-5)$
さっきと逆で解いていきましょう。
Pはx方向に左に4、y方向に上に1進んだ場所。Qはx方向に左に2、y方向に下に5進んだ場所に点を打てばOKです。答えは下図のようになります。
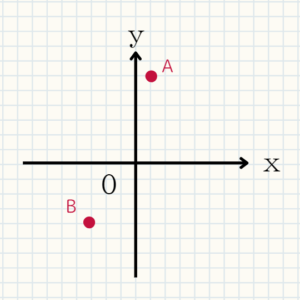
確認問題57
次の2点A,Bの座標を求めよ。また、$C(2,-3)$の点を図にかけ。
いかがでしたでしょうか?
次回は「比例のグラフの書き方と読み取り方」を学んでいきます!
それでは、また次回でお会いしましょう( ^_^)/~~~
確認問題の答え
確認問題56
(2)と(4)
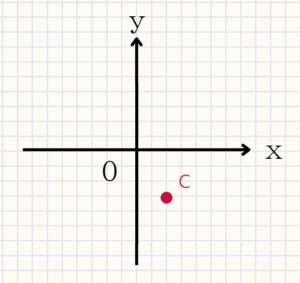
確認問題57
$A(1,6)$
$B(-3,-4)$


コメント