範囲のある比例のグラフと反比例

前回は「比例のグラフ」について学んでいきました。
今回はその応用と、新しい「反比例」というものについて学んでいきます。

４－５　比例のグラフで範囲のあるもの

今回の範囲があるものとはどういうことかというと、始めと終わりが存在するということです。
例えば、12Lの容器に毎分2Lずつ水を入れるとすると、容器には最初0Lから始まり、12Lで満タンとなり終了です。そして、時間も0分から始まり、6分で終わります。

このような時には変域という言葉を使い、不等号で表現します。
例えば、容器の水をyL、時間をx分とすると、
$0\leqq x \leqq 6$
$0\leqq y \leqq 12$
とそれぞれ表すことができます。

例題６

駅から山小屋までの全長12kmのハイキングコースを時速4kmで歩くことにした。
現在、スタート地点の駅にいて、x時間後に駅からykmの地点にいるとき、次の問いに答えなさい。
（１）yをxを使って表せ。
（２）x,yの変域をそれぞれ求めよ。
（３）x,yの関係をグラフで表せ。

（１）距離＝速さ×時間なので、
$y=4x$となる。簡単ですね。

（２）早速出てきました、変域。始まりと終わりでしたね。
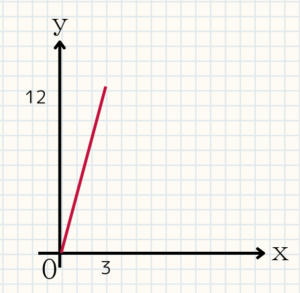
$0\leqq x \leqq 3$
$0\leqq y \leqq 12$

（３）最後にグラフです。（２）で求めた変域の場所だけになるので、下図のようになります。これが、範囲のある比例のグラフです。

確認問題６０

ノート１ページに底辺の長さがxcm、高さが1cm、面積がycm²の三角形を1つかく。ただし、ノート1ページのかくことのできる範囲は、縦、横ともに13cmの正方形とする。次の問いに答えよ。
（１）yをxを使って表せ。
（２）xの変域を求めよ。
（３）x,yの関係をグラフで表せ。
（４）yの変域を求めよ。

４－６　反比例

この節からは反比例を学んでいきます。
反比例とは、xが2倍、3倍…になれば、yが1/2倍、1/3倍となる関係のことを言います。

例えば、1人で行うと6時間かかる作業を、2人で行うと3時間で済みますよね。
これをx人で、y時間かかるとすると下表のようになります。

人数（x人）	1	2	3	6
作業時間（y時間）	6	3	2	1

このとき、xとyの関係は
$xy=6,y=\frac{6}{x}$と表すことができます。

このように反比例の式は$xy=a,y=\frac{a}{x}$と表すことができます。
$a$は比例定数と呼ぶのは変わりません。

それでは確認問題に挑戦して終わりにしましょう！

確認問題６１

次のうち、x,yが反比例の関係になっているものをすべて挙げ、その比例定数を答えよ。
（１）$xy=7$
（２）$x^2y=9$
（３）$x+y=-5$
（４）$y=-\frac{2}{x}$

いかがでしたでしょうか？
次回は「反比例のグラフ」を学んでいきます！
それでは、また次回でお会いしましょう( ^_^)/~~~

確認問題の答え

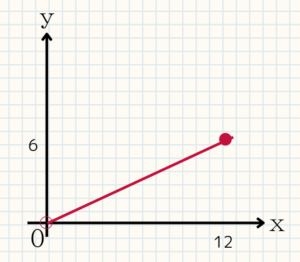
確認問題６０

（１）$y=\frac{1}{2}x$
（２）$0 < x \leqq 13$
（３）下図
（４）$0 < y \leqq \frac{13}{2}$

確認問題６１

（１）と（４）が反比例の関係である。
（１）の比例定数は$7$
（４）の比例定数は$-2$