反比例のグラフ

前回「範囲のある比例のグラフと反比例」について勉強していきました。
今回は「反比例のグラフ」を学んでいきます。反比例とは何かは前回の記事で紹介しています。

４－７　反比例のグラフをかいてみよう

例題７

$y=\frac{4}{x}$のグラフをかけ。

比例の時の同じように、まずは表で考えていきましょう。

x	-4	-3	-2	-1	0	1	2	3	4
y	-1	$-\frac{4}{3}$	-2	-4	×	4	2	$\frac{4}{3}$	1

分母が０になることはないので、×をつけてあります。グラフにプロットとして結ぶと下図のようになります。

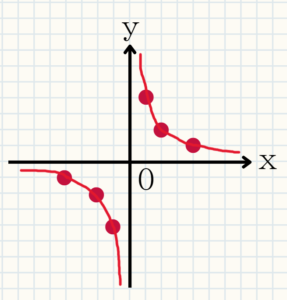
このように二つの曲線になることを双曲線と呼びます。

例題８

$y=-\frac{6}{x}$のグラフをかけ。

同じように表から求めていきましょう！

x	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
y	1	$\frac{6}{5}$	$\frac{3}{2}$	2	3	6	×	-6	-3	-2	$-\frac{3}{2}$	$-\frac{6}{5}$	-1

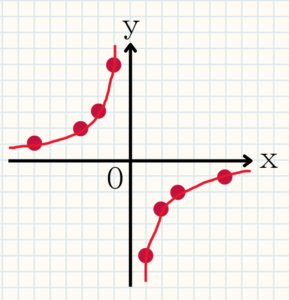
反比例のグラフのまとめ

$y=\frac{a}{x}$のグラフは
比例定数の$a$が正のときは、右上と左下
比例定数の$a$が負のときは、右下と左上
に双曲線のグラフができる。

それでは最後に確認問題に挑戦です。

確認問題６２　次のグラフをかけ

（１）$y=\frac{8}{x}$
（２）$y=-\frac{3}{x}$

４－８　グラフから反比例の式を求める

例題９　次の反比例のグラフの式を求めよ

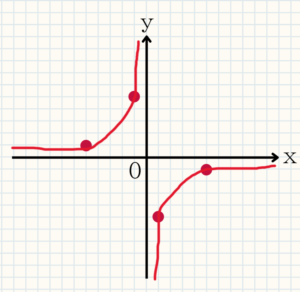
グラフから式を読み取る方法は比例の時と同じです。
通る点を基本の式に代入します。$y=\frac{a}{x}$を用いてもよいですが、$a=xy$で求めると計算がしやすいです。
このグラフは点$(-5,1)$を通るので、$a=-5\times 1=-5$なので、
$y=-\frac{5}{x}$が答えとなります。

確認問題６３　次の反比例のグラフの式を求めよ

４－９　反比例のグラフで範囲のあるもの

例題１０

容積480Lの空っぽのふろおけに1分間にxLの割合でお湯をいれると、いっぱいになるのにy分かかる。ただし、蛇口は全開にしても1分間に40Lまでしか出ないとする。次の問いに答えよ。
（１）yをxを使って表せ。
（２）xの変域を求めよ。
（３）x,yの関係をグラフで表せ。
（４）yの変域を求めよ。

（１）xとyを掛け合わせると満タンの480Lになるので、
$xy=480$よって、$y=\frac{480}{x}$

（２）蛇口は全開にしても1分間に40Lまでしか出ないとあるので
$0<x\leqq 40$

（３）このグラフは点$(40,12)$を通るので下図のようになります。

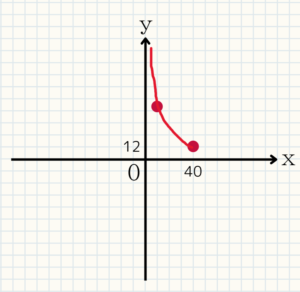
（４）yの変域はグラフから読み取れますね。
$y\geqq 12$となります。

確認問題６４

かおりさんは、50mの短距離のコースを秒速xmで走ると、y秒かかる。また、全力で走っても10秒かかるとする。次の問いに答えよ。
（１）yをxを使って表せ。
（２）yの変域を求めよ。
（３）x,yの関係をグラフで表せ。
（４）xの変域を求めよ。

いかがでしたでしょうか？
次回は「比例と反比例の文章問題」を学んでいきます！
それでは、また次回でお会いしましょう( ^_^)/~~~

確認問題の答え

確認問題６２

確認問題６３

$y=\frac{2}{x}$

確認問題６４

（１）$y=\frac{50}{x}$
（２）$y\geqq 10$

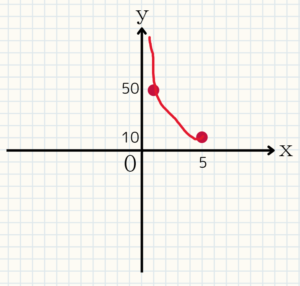
（４）$0<x\leqq 5$