0−7 工夫した計算
ちょっとコラム的な内容になります。一見複雑な計算も工夫をすることで簡単に解けるようになります。早速例題を見ていきましょう!
例題7
次の計算をせよ。
(1)$5+26-9+3-5-18+9$
(2)$19-4-7+3-10+8$
(3)$7\times25\times4$
(1)ここでのポイントは同じものを足して、引くと打ち消すことができるです。
足し算引き算は順番を変えてもOKなので、式を並び替えて簡単にしていきましょう!
$(5-5)+26+(-9+9)+3-18=26+3-18=11$
(2)ここでのポイントは足し算同士と引き算同士を分けて考えることです。
足し算引き算は順番を変えてもOKなので、式を並び替えて簡単にしていきましょう!
$19-4-7+3-10+8=(19+3+8)-(4+7+10)=30-21=9$
(3)ここでのポイントは計算をしやすい数を作ることです。
今回の場合は100を作っていきましょう!
$7\times25\times4=7\times(25\times4)=7\times100=700$
かなり計算が楽になったのではないでしょうか?最後に確認問題を解きましょう!
確認問題7
次の計算をせよ。
(1)$14-3+8-6-8+3$
(2)$94-20+18+6+32$
(3)$8\times2\times9\times5$
0−8 速さ・時間・距離
小学校でも大切な単元の一つでしたね。中学校になってからも方程式という単元などで使うのでしっかり復習していきましょう!
距離=速さ×時間
速さ=距離÷時間
時間=距離÷速さ
上の式だと分かりづらいですよね。そこで下のような図で覚えていきましょう!
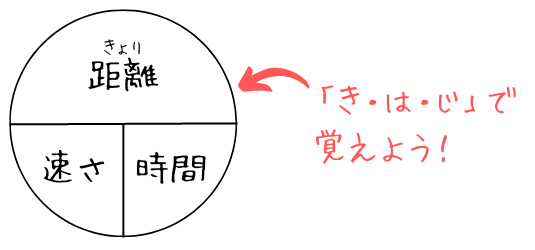
例題8
次の問いに答えよ。
(1)時速4kmで2時間歩いたときの距離は何kmになるか。
(2)5分で1000m進む速さは分速何mか。
(3)秒速4mで200m歩くには何秒かかるか。
(4)分速21kmで音が伝わるとすると、音源から700m離れた場所までは何秒で伝わるか。
(1)距離は速さ×時間なので、$4\times2=8km$
(2)速さは距離÷時間なので、$1000\div5=分速200m$
(3)時間は距離÷速さなので、$200\div4=50秒$
(4)は少し注意が必要です。
速さの単位が違うので、他と合わせないといけません。つまり「分速●km」を「秒速●m」に直します。
分速21km=分速21000m=秒速350m(21000÷60)
時間は距離÷速さなので、$700\div350=2秒$
このように単位に注目するのは文章題では必須です!
最後に確認問題に挑戦しましょう。
確認問題8
時速4.8kmで11分歩いた距離は何mか。
いかがでしたでしょうか?
次回からは図形の分野、三角形、四角形、円の面積のおさらいをしていきます。
それでは、また次回でお会いしましょう( ^_^)/~~~
確認問題の答え
確認問題7
(1)8
(2)130
(3)720
確認問題8
分速880m


コメント