前回は「比例と座標」とは?ということを学んでいきました。
今回は実際に比例のグラフを書いてみたり、読み取ってみたりしましょう!
4-3 比例のグラフを書いてみよう
例題3
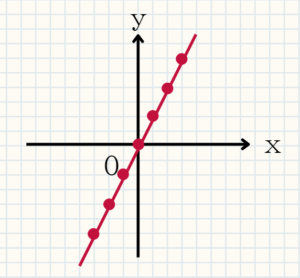
$y=2x$のグラフをかけ。
さて早速グラフを書いてみましょう!まずは表で表してみましょう。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
そして前回ちらっとお伝えしましたが、点の集合が線になるので、上記の表をプロットして、つなげればグラフの完成です!
それでは、もう1問解いてみましょう!
例題4
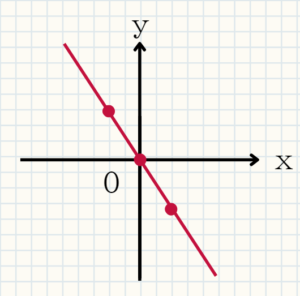
$y=-\frac{3x}{2}$のグラフをかけ。
同じように表にして確認しましょう。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9/2 | 3 | 3/2 | 0 | -3/2 | -3 | -9/2 |
分数が多いですが、大丈夫。2点が分かっていれば線を引くことができます。
比例のグラフのまとめ
$y=ax$のグラフは
比例定数の$a$が正のときは、右上がりの増加のグラフ
比例手数の$a$が負のときは、右下がりの減少のグラフ
となる。
※グラフは原点ともう1点が分かれば書くことができる。
確認問題58 次のグラフをかけ
(1)$y=3x$
(2)$y=-\frac{x}{4}$
4-4 グラフから比例の式を求める
次にグラフから比例の式を求めてみましょう。ヒントは原点ともう1点が分かればグラフはかけるということです。
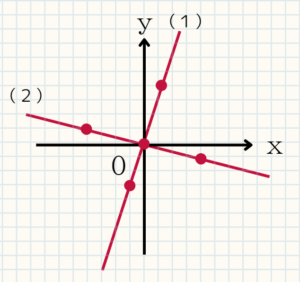
例題5 次の(1)(2)の比例のグラフの式を求めよ
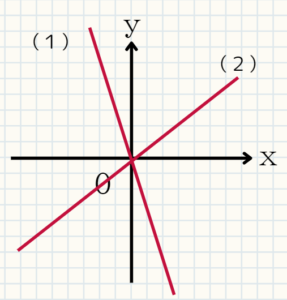
通る点を見ていきましょう。(1)は$(-1,3)$を(2)は$(4,3)$を通ることが分かります。
これを比例の式$y=ax$に代入して、$a$を求めれば、比例の式が完成します。具体的にやっていきましょう。
(1)$3=-1\times a$
$a=-3$
よって、$y=-3x$
(2)$3=4 \times a$
$a=\frac{3}{4}$
よって、$y=\frac{3}{4}x$
それでは確認問題に挑戦です!
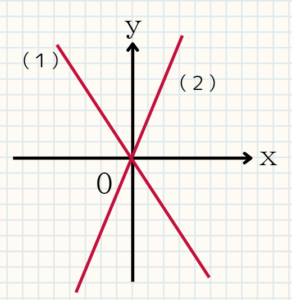
確認問題59 次の(1)(2)の比例のグラフの式を求めよ
いかがでしたでしょうか?
次回は「範囲のある比例のグラフと反比例」を学んでいきます!
それでは、また次回でお会いしましょう( ^_^)/~~~
確認問題の答え
確認問題58
確認問題59
(1)$y=-x$
(2)$y=\frac{5}{2}x$


コメント